Zenón de Elea fue un filósofo griego que vivió unos 4 siglos antes de Cristo. Es conocido por sus paradojas, algunas de las cuales niegan la existencia del movimiento. Zenón intentó probar que el espacio no está formado por elementos discontinuos y, concretamente, que no existe el movimiento. La paradoja de Aquiles y la tortuga, o la paradoja de la flecha han llegado hasta nuestros días y siguen atormentando a los estudiantes de filosofía.
-
-
No es mucho lo que se sabe sobre la vida de Zenón de Elea, ya que se conservan muy pocos fragmentos y casi todos ellos son referencias indirectas de otros autores que mencionan hechos o situaciones que se le atribuyen. La fecha de su nacimiento tampoco es segura, pero se acepta que nació entre el año 490 y el 485 antes de Cristo. Los razonamientos de Zenón, que fue discípulo de Parménides y tuvo una formación pitagórica, constituyen el primer intento del pensamiento infinitesimal, que solo fue desarrollado en profundidad unos dos mil años después por Leibniz y Newton.
Las paradojas de Zenón son una serie de paradojas ideadas para demostrar que las sensaciones que obtenemos del mundo son ilusorias y no existe el movimiento. Zenón repetía a quien quisiese escucharlo que una persona no podía recorrer ninguna distancia en absoluto, aunque los sentidos mostrasen que tal cosa era posible. Sus ideas pertenecen a la categoría de paradojas falsídicas, también conocidas como sofismas. Esto significa que alcanzan un resultado que es falso, culpa de una falacia en el razonamiento, generalmente producto de la falta de conocimientos sobre el concepto de infinito en la época en la que fueron formuladas.
Segun Zenón, Aquiles nunca alcanzará la tortuga.
Aquiles y la tortuga
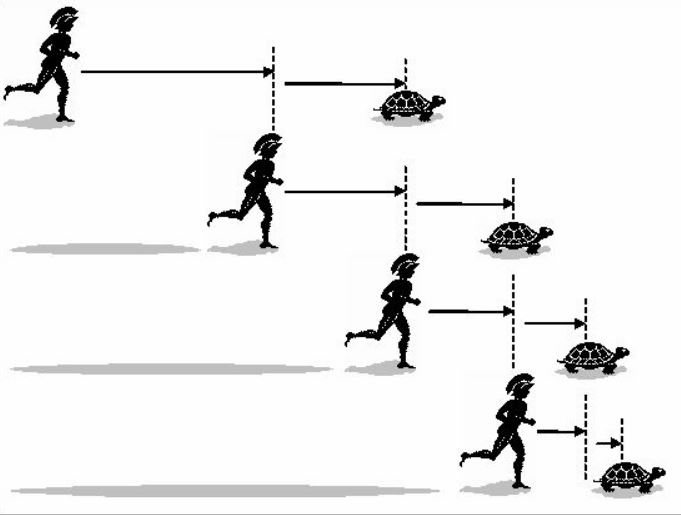
Aquiles y la tortuga es, quizás, la más conocidas de las paradojas de Zenón. El filósofo argumentaba que, en una hipotética carrera entre Aquiles (el guerrero que mató a Héctor) y una tortuga, si esta tenía última una ventaja inicial, el humano siempre perdería. Zenón “demostraba” que, a pesar de que el guerrero corre mucho más rápido que la tortuga, nunca podría alcanzarla. Imaginemos que la distancia a cubrir en la carrera son cien metros, y que la tortuga tiene cincuenta metros de ventaja. Al darse la orden de salida, Aquiles recorre en poco tiempo la distancia (cincuenta metros) que los separaba inicialmente. Pero, al llegar allí, descubre que la tortuga ya no está, sino que ha avanzado, mucho más lentamente, diez o veinte centímetros. Lejos de desanimarse, el guerrero sigue corriendo. Pero, al llegar de nuevo donde estaba la tortuga, ésta ha avanzado un poco más. Zenón sostiene que esta situación se repite indefinidamente, y que Aquiles jamás logrará alcanzar a la tortuga, que finalmente ganará la carrera.
Es bastante obvio que esto no es así, y es muy fácil comprobar en la práctica que dicho razonamiento es erróneo. Sin embargo, no es tan fácil encontrar donde está el fallo, y hubo que esperar hasta mediados del siglo XVII para que el matemático escocés James Gregory demostrara matemáticamente que una suma de infinitos términos puede tener un resultado finito. Los tiempos en los que Aquiles recorre la distancia que lo separa del punto anterior en el que se encontraba la tortuga son infinitos, pero cada vez más y más pequeños. La suma de todos estos tiempos, a pesar de su infinito número, da como resultado un lapso de tiempo finito, que es el momento en que Aquiles alcanzará a la tortuga.
Otra forma de encarar el problema es evitando el análisis infinitesimal utilizando el análisis discreto. Podemos pensar que Aquiles no recorre espacios infinitesimales, sino discretos, que podemos llamar “zancadas”. A cada zancada le corresponde una distancia concreta de, por ejemplo, un metro. De esa manera, el problema se reduce a calcular en qué momento la última zancada de Aquiles recorrerá una distancia mayor a la que haya podido recorrer la tortuga en el mismo tiempo. De esta forma se puede demostrar que, como hoy sabemos, el movimiento existe.
Dificilmente pueda ganarle una carrera a Aquiles.
La paradoja de la flecha
Esta otra paradoja implica el lanzamiento de una flecha. Zenón afirmaba que, en cada instante, la flecha está en una posición del espacio determinada. Si el periodo de tiempo considerado es lo suficientemente pequeño, la flecha no alcanzará a moverse, por lo que está en el reposo durante ese instante. Ahora bien, el mismo razonamiento puede aplicarse a los restantes infinitos de periodos de tiempo, en los que la flecha también estará en reposo por el mismo motivo. De esta forma Zenón demostraba que el movimiento de una flecha es imposible, a pesar de que miles de viudas cuyos maridos habían muerto de un flechazo en el campo de batalla le insistieran con lo contrario.
La paradoja puede evitarse de varias maneras. Una de ellas es simplemente pensar que cada instante en que la flecha se percibe como “en reposo” es un algo relativo. No se puede juzgar, observando sólo una “foto” de un objeto si está o no en reposo. En lugar de ello, es necesario compararlo con los instantes adyacentes, previos y posteriores. Al ver la “película”, podemos determinar que la flecha está en distintas posiciones en cada instante, por lo que -efectivamente- se está moviendo. Otra solución es recurrir a la definición de velocidad, cuya esencia es el cambio. El movimiento es la sucesión de los distintos espacios ocupados por el cuerpo (la flecha), a lo largo de la sucesión de los distintos momentos que componen el total del tiempo considerado. Así, si asumimos que el concepto velocidad, es decir, movimiento, puede definirse racionalmente, simultáneamente estamos admitiendo que el movimiento, racionalmente, en teoría, existe.
En el mundo real, las flechas se mueven sin problemas.
XXV siglos más tarde, nos parece hasta ridículo lo que proponía Zenón. Sin embargo, si pensamos en el estado en que se encontraba la ciencia cuatro o cinco siglos antes de la era Cristiana, los razonamientos de este hombre cobran real magnitud. Debe haber sido sumamente difícil para Zenón reconciliar la (aparente) certeza detrás de sus razonamientos con las evidencias del mundo real, donde la tortuga era invariablemente la perdedora de la carrera, y las flechas llegaban a su blanco.
-
¿Y tú, qué opinas?
-
#1jerryco miércoles, 15 de julio de 2009, 18:22
En el caso de la flecha, lo de la foto no es un argumento en contra, ya que una foto es UN momento. Lo que decia esta persona es que, si tomamos una foto, y luego otra en un instante CASI identico al de la primera, no se habra movimiento de la flecha entre una foto y otra. Si hacemos esto millones de veces, habremos avanzado en el tiempo y sin embargo la flecha "no se habra movido". Es interesante el planteo
-
#2Gabriel miércoles, 15 de julio de 2009, 18:42
Pues esto me parece del todo absurdo, puestos a poner condiciones inutiles hasta la teoria más estrafalaria es cierta.
Además en el caso de Aquiles ¿por que tendira que pararse cada vez que llega adonde supuestamente esta la tortuga y no sigue corriento y punto?
O lo de la flecha... ¡no te fastidia! yo puedo decir que el agua del mar es dulce si se hace un sorbo infinitamente pequeño y no se cosa más -
#3matiiax_x miércoles, 15 de julio de 2009, 18:46
#1La foto amigo, se refiere a que las flechas , a pesar del razonamiento de Zenon, si atraviezan cosas y matan gente..
Offtopic: existe un video, donde se dispara una bala, y esta atravieza muchas cosas, entre ellas frutas, y otros objetos comunes... al final del video esta un niño...
http://www.youtube.com/watch?v=bj6rzV8gSe8 -
#4
-
#5leodan miércoles, 15 de julio de 2009, 19:11
Alguien de ustedes me puede explicar, para que sirve estudiar filosofía? y que se gana al estudiarlo
-
#6
-
#7falcatin miércoles, 15 de julio de 2009, 19:41
Aquiles=linux
tortuga=windows
Zenón de Elea=Bill Gates
Paradoja falsídica=Linux jamás podrá alcanzar a windows
Creo que sí entendí, muy buena información, extraño pensamiento pero es interesante conocerlo. -
#8
-
#9
-
#1153m4 miércoles, 15 de julio de 2009, 22:00
a #5 Pues precisamente no creo que esté tarado, simplemente jugaba con falacias dentro del razonamiento.
a #6 sirve para que pienses por ti mismo y que aunque te equivoques, aprendas y sigas pensando, o prefieres que piensen por tí? (la filosofía es amor al conocimiento) -
#12radamanto3 miércoles, 15 de julio de 2009, 22:02
Lo mejor de esta lectura son los comentarios. Para el que no entiende la filosofia esta si sirve,
para dar clases de Filosofia. -
#13juan03 miércoles, 15 de julio de 2009, 22:05
Aquiles perdía la carrera porque siempre que llegaba donde estaba la tortuga pisaba la tortuga y se lastimaba el talón y eso lo hacia detener siempre.
-
#14Juan Antonio miércoles, 15 de julio de 2009, 22:06
rambaldi87 macho, vives esclavo de linux o que? El mundo no se reduce a linux y el fantastico mundo de virtudes de software libre.
La esencia del mundo, las distintas ramas de las inquietudes de una persona no se reducen a linux ni posibles comparaciones con este, tienen valor propio sin necesidad de ser comparados.
Martinsoft, pues por ejemplo la ciencia, el criterio científico, no es mas que una filosofia, si no se hubiera razonado, no existiria. Ademas se gana comprehension de uno mismo y del mundo que te rodea. -
#15Emilio Munoz miércoles, 15 de julio de 2009, 22:25
#1Hablando infinetisimalmente, es imposible que en la foto tomada después de un instante CASI identico al de la primera no haya variación de espacio. El 'CASI' ya implica una variación de tiempo y, por mas pequeño que sea, implica ya un desplazamiento. Y si hacemos esto millones de veces, SIEMPRE habrá movimiento, solo que a una escala menos perceptible de una foto a su siguiente. Si de ese millon de fotos tomas 1 cada 100.000 y las comparas, probablemente notes alguna diferencia... x=vt. Si t varía y v es cte entonces x varía, sin importar lo pequeña q sea esa diferencia.
-
#16
-
#17jmymyr miércoles, 15 de julio de 2009, 22:50
don't start the flame war.....
y al pensar en todas estás falacias y paradojas uno se pone a pensar en los supuestos "argumentos" que prueban la existencia de diós, como la necesidad de una causa sin causa, la necesidad de un legislador para que existan las leyes naturales, la necesidad de un creador inteligente para un universo inteligible,
aquí va algo para los enlaces recomendados de la semana:
http://bardruck.blogspot.com/2008/05/argumentos-que-prueban-la-existencia-de.html
-
#18Ciul miércoles, 15 de julio de 2009, 22:58
Si se quiere uno dar mala vida como aquellos que le prestaban atención al Sr Zenón, pues entonces piensen esto:
"Uno no puede decir que el presente exista puesto que toda reacción que éste produjera tardaría en ser percibidos por nuestros sentidos y luego enviado y procesado por el cerebro, por más insignificante que nos parezca ese lapso de tiempo. Una vez calculé cuánto tarda la luz solar en viajar del Sol a un objeto terrestre en frente mio y rebotar a mis ojos para que así mis ojos puedan percibir el color y deducir que allí existe un objeto."
Esto en su momento me conmocionó y causó impresión en mi. -
#19jerryco miércoles, 15 de julio de 2009, 23:20
#5Todo el sistema de razonamientos y sistemas que rigen nuestra vida actual (e incluso los alternativos) surgen de la filosofia.
Es a traves del pensamiento filosofico que surgen sistemas como el capitalismo, el comunismo, el utilitarismo, el existencialismo, que es el bien y que es el mal, la justicia, porque es bueno hacer el bien y malo hacer el mal... podriamos hablar eternamente sobre sus beneficios -
#20andres miércoles, 15 de julio de 2009, 23:34
Se ve a los compas lectores no han tenido un buen día. Me acuerdo de un profesor de Analasis Matematico I, el cual siempre decia la paradoja de la tortuga y Aquiles, y como en su infancia cuando se la contaron no podia demostrar lo contrario, creo que a lo que iba con esto, es que es facil dar por ciertas las cosas, lo dificil es demostrarlas. No se seguro es una boludes pero para mi estaba bueno (aclaro, quedense tranquilos los pesimistas, que no era justamente esto lo que teniamos que demostrar). Haber si tambien la ligo.
-
#21ferpar jueves, 16 de julio de 2009, 00:15
#5La filosofia, mi amigo martinsoft, se estudia para enseñar filosofia. yo creo que es la unica profecion recursiva que hay. XD
-
Cargando...
-
nuevo comentario
Nombre Campo obligatorio
Email Escriba una dirección de correo electrónico con el formato sunombre@ejemplo.com.
Campo obligatorio
-
