El matemático británico John Horton Conway es considerado -con justicia- uno de los mayores creadores y divulgadores de pasatiempos matemáticos de todos los tiempos. Una de sus más interesantes contribuciones es el denominado “algoritmo del día del fin del mundo”, que permite determinar -mentalmente y en menos de 30 segundos- qué día de la semana fue o será una fecha cualquiera del calendario Gregoriano. Hoy te mostramos, paso a paso, cómo realizar ese truco.
Es posible que alguna vez hayas visto en la tele algún “mentalista” adivinar que día de la semana corresponde a una fecha cualquiera, proporcionada por el conductor o alguna llamada telefónica. Seguramente habrás imaginado que detrás de todo el numerito montado por el “artista” había un algoritmo lo suficientemente simple como para ser “ejecutado” mentalmente, sin errores y en unos pocos segundos. Dicho sistema existe, y ha sido diseñado por uno de los matemáticos especializados en divulgación y pasatiempos más famoso de todos los tiempos: John Horton Conway.
John Horton Conway
Este británico, de 80 años, es una verdadera leyenda viviente, responsable de cientos de pasatiempos y acertijos sumamente interesantes. Uno de ellos es el que le permite “adivinar” que día de la semana fue (o será) una fecha cualquiera. Se dice que la clave de su ordenador se basa en este algoritmo: la máquina le muestra una fecha aleatoria y en menos de 30 segundos Conway debe responder que día de la semana fue. Obviamente, como protección dista mucho de ser segura, ya que cualquier instruso con un segundo ordenador y un software de calendario a mano podría responder a la pregunta planteada sin problemas, pero Conway lo utiliza como una forma de “mantener su mente despierta”. El matemático ha denominado a su sistema como “algoritmo del día del fin del mundo” (“Doomsday algorithm” o “Doomsday rule”). Veamos en que consiste y cómo se usa.
Obviamente, como protección dista mucho de ser segura, ya que cualquier instruso con un segundo ordenador y un software de calendario a mano podría responder a la pregunta planteada sin problemas, pero Conway lo utiliza como una forma de “mantener su mente despierta”. El matemático ha denominado a su sistema como “algoritmo del día del fin del mundo” (“Doomsday algorithm” o “Doomsday rule”). Veamos en que consiste y cómo se usa.
Algoritmo del día del fin del mundo
El funcionamiento del “Doomsday algorithm” se basa en la premisa de que para cualquier año existen una serie de fechas fáciles de recordar que “caen” siempre en el mismo día de la semana. Los años bisiestos -aquellos en que Febrero tiene 29 días- suponen una complicación adicional, ya que todas las fechas posteriores a ese día se “corren”, pero Conway evita este problema de la misma forma en que hacían los romanos: considerando el primer día del año al 1 de Marzo, y como “fin de año” el último día de febrero. Las fechas que debemos recordar son las siguientes:
- El “0”de Marzo” (el último día de Febrero, en realidad),
- El 4 de Abril,
- 9 de Mayo
- 6 de Junio
- 11 de Julio
- 8 de Agosto
- 5 de Septiembre
- 10 de Octubre
- 7 de Noviembre
- 12 de Diciembre
- 2 de Enero (del año siguiente)
- 13 de Febrero (del año siguiente)
¿Crees que es imposible recordar esas fechas? Pues te equivocas. Si miras con detenimiento la lista anterior, notarás que -dejando de lado los meses de Enero y Febrero, todas las correspondientes a meses pares tienen la forma “n/n” :4/4, 6/6, 8/8, 10/10 y 12/12. Y las que corresponden a los meses impares son 9/5, 11/7, 5/9 y 7/11. Estas cuatro pueden resultar un poco más difíciles, pero los anglosajones lo tienen fácil gracias al mnemónico “I work from 9 to 5 at the 7-11“( o “Trabajo de 9 a 5, en el Seven-Eleven“, donde “Seven-Eleven” es una cadena de tiendas muy famosas en Estados Unidos). Como sea, esa frase nos permite recordad las cuatro fechas en cuestión. Y la dos restantes corresponden al día de la toma de Granada y la víspera de San Valentín, así que con poco trabajo lograrás memorizar la lista.
Esas fechas, como te adelantamos, caen todas en el mismo día de la semana, y Conway las denomina “Día del Juicio“, de donde proviene el nombre del algoritmo. Determinando que día de la semana es el que corresponde para el año de la fecha que queremos “adivinar”, podemos calcular sin problemas el dato que estamos buscando.
Para encontrar el “Doomsday” aprovechamos que el calendario Gregoriano (si, el mismo que usamos todos los días en nuestra vida cotidiana) se repite cada 400 años, o lo que es lo mismo, cada cuatro siglos. Para simplificar los cálculos, vamos a asumir que cada siglo comienza enlos años acabados en “00” y finalizan en los años acabados en “99“. Conway llama al primer “Doomsday” de cada siglo “marcador de siglo”, y se repite cada 400 años. Esos días son:
- Siglo 1800-1899: Viernes
- Siglo 1900-1999: Miércoles
- Siglo 2000-2099: Martes
- Siglo 2100-2199: Domingo
Veamos ahora como calcular el “Doomsday” de un año cualquiera. Si llamamos “y” a los dos últimos dígitos del año en que estamos trabajando, el “Doomsday” correspondiente se calcula con la siguiente fórmula:
Antes que cierres el navegador espantado por semejante sarta de símbolos matemáticos, lee la siguiente explicación: El Doomsday se calcula sumando al marcador del siglo el resultado de la división (sin tener en cuenta los decimales) entre los dos últimos dígitos del año y 12, más el resto de dicha división, más ese mismo resto dividido 4. En otras palabras, tomamos “y”, lo dividimos por 12 para obtener un cociente (“g”) y un resto (“r”). A “r” lo dividimos por 4 y obtenemos un nuevo cociente (“s”). El “Doomsday” del año es igual a y+q+r+s. Si ese valor es mayor que 7 (algo muy probable) lo dividimos entre 7 y nos quedamos con el resto. ¡Es fácil!
Veamos un ejemplo. Supongamos que queremos calcular que día de la semana fue el 14 de Octubre de 1968. El marcador para ese siglo (1900-1999) es Miércoles, y el valor de “y” es 68, que al dividir entre 12 nos da 5, con resto 8. IMPORTANTE: Ese resto de “8” es equivalente calcular “68 MOD 12” (68 módulo 12) . Al dividir el resto entre 4 nos da 2, así que el “Doomsday” es igual a 5 + 8 + 2 = 15. Dividimos por 7 y obtenemos el resto: 1 (O hacemos 15 MOD 7, que tambien debe dar 1). Como el marcador de ese siglo es Miércoles, el 10/10 nuestra referencia para ese mes, y 1 nuestro “Doomsday”, contamos hacia delante 1 día: Jueves.
El 10/10/1968 fue Jueves. El 11 fue Viernes, el 12 Sábado, el 13 Domingo y el 14 Lunes. Es decir, el 14 de Octubre de 1968 es Lunes. ¿Interesante, verdad? Otro ejemplo rápido: hoy es 12 de Noviembre de 2010 ¿Que día de la semana es? Fácil: Marcador de siglo: Martes. “Doomsday” igual a 5 (te dejamos calcularlo a ti, recuerda que para 2010 “y” = 10). El 7/11 es nuestro marcador más cercano, y es Domingo (5 días contando a partir de Martes). Si el 7/11 fue Domingo, el 12/11 es Viernes.
Sabiendo todo esto: ¿Te animas a calcular que día de la semana fue cuando naciste?






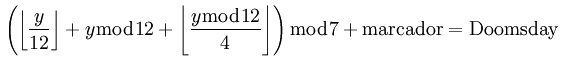


¡Que chulo! Mi madre me dijo que nací un viernes… 27/08/84 y la respuesta es…. ¡Viernes! Mi madre no me mintió XD.
No espera…. ¡¡era miércoles!! Maldita sea xD.
Pues no lo entiendo, según el calendario del ordenador era lunes XDDD. A ver: El marcador es Miércoles, y=84, que entre 12 da 7 con resto 0, 0/4 sigue siendo 0, 84+7=91, divido entre 7 y me da resto 0. Si el marcador es Miércoles sigue siendo el mismo día ¿¿no?? Osea que según eso el 27 de Agosto de 1984 fue Miércoles…. algo falla xDD.
siii algo fallaaaa!!
TU CEREBROOO DE MIERDA ES EL QUE ESTÁ FALLANDO!!
A ver si sale..
Marcador del siglo: Miercoles.
Fecha más cercana para Doomsday: 8/8
Doomsday= 84+7+0= 0
Eso significa que el 8/8 fue Miercoles (el calendario de mi ordenador confirma esto). Si naciste el 27/8, debes calcular a partir de saber que el 8/8 fue Miercoles…Una semana mas tarde seria 15/8, dos semanas mas tarde 22/8 y miercoles tambien, el 23 jueves….etc,etc y finalmente, el 27 fue lunes.
Conclusion: El ordenador tiene bien la fecha, el algoritmo funciona, tu madre no recordaba la fecha, y tu olvidaste el ultimo paso para realizar el cálculo: sumar los dias transcurridos a partir del 8/8 hasta el 27/8 que era la fecha buscada 🙂
¿Se entendió algo?
Saludos!
Genial xD
Pero es que al darte 0 quiere decir que no debes contar nada asi que simplemente es miercoles y ya.
Tu madre y el ordenador te mintieron. Toda tu vida es una mentira, a llorar al rio. a
Hola,
Yo hice hará unos años un algoritmo para calcular el día de la semana. Aquí dejo mi manual (a mi modo de ver es más sencillo) http://bit.ly/a8bict
Saludos
Q idiotes!
No sabía que había un tipo más idiota que Paenza.
Siempre puede aparecer un imbécil mayor.
Es un principio matemático que empieza aquí y posee crecimiento exponencial.
esto lo dice una "persona" que tiene como avatar una foto de kramer un personaje gracioso pero de lo mas estupido en la serie seinfield.
Como yo ! Jajaja mira que soy imbecil !
me pareció ver un argumentum ad hominem más arriba??
idiota…
La respuesta es 42
¡¡VIVA MÉXICO CABRONES!!
no mames, con personas como tu hasta pinche pena ajena da, decir que soy mexicano…
O sea si la formuka es doomsday= (y + (y mod 12) +((y mod 12)/4))mod 7 + marcador de siglo, siendo y los ultimos dos digitos del año, entonces me parece que la imagen que subiste está mal….
Mas bien las operaciones que hace en el ejemplo son confusas, la imagen con la ecuación es correcta, intente por todas las maneras posibles sus ejemplos y no da pero siguiendo tal cual la ecuación ya lo pude resolver.
El el 14 de Octubre de 1968 fue Martes y en el texto lo calculaste como Lunes.
Trate de hacer lo mismo para el 8 de Abril de 1983 y da Domingo cuando realmente fue Viernes.
Hola Jrecma!
El 14 de Octubre de 1968 efectivamente fue LUNES…
Puedes verlo en el calendario del ordenador 😉
Saludos!
jajajaja que incomodo, windows 7 me pone que es martes
podrias calcularlo para el 8 de abril de 1983 ? me da domingo, te da igual?
A ver creo que tus calculo están mal pero el resultado es correcto:
Y=68;
Marcador=3;
([68/12]+68mod12+[68mod12/4])mod7+3
(5+8+2)mod7 + 3 = 4 = DoomsDay = jueves
Entonces 10/10 = jueves
Por lo tanto:
14/10 = lunes
m epueden ayudar con el 14 febrero del 2011? es que no me sale para esa fecha =( Por favor 🙂
A ver, como es febrero tienes que tomar el año "2010", segun la formula tenemos (0+10+2)=12, 12mod 7 = 5, asi que segun el marcador de siglo que es martes tenemos martes + 5 = domingo, asi que las fechas "fijas" de ese año son todas domingo. La mas cercana es el 13 de febrero, es decir, el 13 de febrero es domingo por lo tanto el 14 debe ser lunes cosa que concuerda con mi calendario.
A ver, siguiendo la ecuación término por término: 14 / 02 / 2011
y= 11
quedamos en que el marcador para este siglo es martes cierto?
ademas nuestra referencia de febrero es el 0 de marzo no? igual al 28 de febrero
hacemos números siguiendo la ecuación
primer término, parte entera del cociente de dividir 11/12: 0
segundo termino, el resto de dividir 11/12: 11
tercer termino, parte entera del cociente de dividir 11/5: 2
sumamos todo 0+11+2=13
Ahora nos quedamos con el resto de dividir 13/7: 6
Ahora lo sumamos al marcador que es martes + 6 = Lunes por lo que el 28 de febrero es lunes.
¿Quieres saber que día va a ser el 14 de febrero de 2011?: 28 lunes, 27 domingo, 26 sábado, 25 viernes, 24 jueves, 23 miércoles, 22 martes, 21 lunes, 20 domingo, 19 sábado, 18 viernes, 17 jueves, 16 miércoles, 15 martes, 14 LUNES.
Mas claro ni el agua 🙂
Muchas Graciaaaas, ya me saalió =)
"…Se dice que la clave de su ordenador se basa en este algoritmo: la máquina le muestra una fecha aleatoria y en menos de 30 segundos Conway debe responder que día de la semana fue.
Obviamente, como protección dista mucho de ser segura, ya que cualquier instruso con un segundo ordenador y un software de calendario a mano podría responder a la pregunta planteada sin problemas, pero Conway lo utiliza como una forma de “mantener su mente despierta”…."
Disculpen, pero eso carece de cualquier sentido literario, de que idioma esta traducido, arameo ?
Alguien podria dar otro ejemplo, por mas que intento no logro comprender….. me interesa dilucidar esto…
Ultimo ejemplo por hoy 🙂
25 de diciembre de 2010:
El marcador mas cercano es el 12/12, y para este siglo el dia "base " es Martes. Los dos dígitos del año son 10. Esos son nuestros datos.
Ahora haces: 10/12 = 0 ; 10 MOD 12 = 10; 10/4 = 0. Sumamos 0+10+2 y nos da 12. "12 MOD 7" = 5. Contamos 5 días a partir del Martes, y tenemos que el 12/12/2010 es DOMINGO.
Si el 12/12 es domingo, siete dias mas tarde, el 19/12 vuelve a ser domingo, el 20 lunes, 21 martes…….y el 25 es SABADO.
El ordenador (con Ubuntu 10.10) me dice exactamente lo mismo. Lo mismo me pasa con el ejemplo del 14/10/68 (ya sabeis que soy un vejestorio): Es LUNES. Ignoro por que Win7 dice otra cosa. 🙂
Prueben primero con un lapiz y papel, cuidando de usar los datos correctos, y cuando lo dominen bien, recien intentarlo mentalmente. Son calculos sencillos, pero al ser varios encadenados, es facil equivocarse.
Suerte!
Hablando de equivocarse….puse "10/4 = 0. Sumamos 0+10+2… " y debería ser "10/4 = 2. Sumamos 0+10+2… ". Me equivoque al tipear lo que tenia en un papel…….ja ja ja!. Pero el resultado está bien por que la suma la copie bien.
¡Voy a soñar con esto!
"Supongamos que queremos calcular que día de la semana fue el 14 de Octubre de 1968. El marcador para ese siglo (1900-1999) es Miércoles, y el valor de “y” es 68, que al dividir entre 12 nos da 5, con resto 8. Al dividir el resto entre 4 nos da 2, así que el “Doomsday” es igual a 68 + 5 + 8 + 2 = 83. Dividimos por 7 y obtenemos el resto: 6. Como el marcador de ese siglo es Miércoles, el 10/10 nuestra referencia para ese mes, y 6 nuestro “Doomsday”, contamos hacia delante 6 días: Miércoles, Jueves, Viernes, Sábado, Domingo y Lunes. Es decir, el 14 de Octubre de 1968 es Lunes."
no se supone q usamos la formula para encontrar el dia del doomsday y no el dia de la fecha que nos estas pidiendo? Contaste 6 dias desde el marcador del año porque a eso dio la formula usando la terminacion 68 sin usar el 14. Y a eso dio Lunes, pero y si hubiera sido 15 o 16 de octubre? siempre le hubieramos tenido que sumar 6 al marcador y no 7 o 8. me podrias explicar mejor porfavor o decirme en que estoy equicovado…gracias
Mientras escribías esto, yo corregía el texto….estaba más que liado. Max también me lo había hecho notar. Creo que ahora está más claro.
Muchas gracias por aclararlo. Esta visto que si mi ordenador me obliga a hacer esto para poder usarlo, no lo podría usar nunca!! 😛
Hay que ver también que no hay una sola forma de hacer los cálculos. Si miras un poco por la web, encontraras varias formas muy parecidas de sumar y contar que al final dan lo mismo. Eso es no solo porque el sistema ha sido modificado muchas veces a gusto del matemático de turno, sino por que algunas operaciones pueden hacerse en otro orden y obtener el mismo resultado.
La explicación más concisa y clara es la fórmula de la figura de la Wikipedia, aunque asume que sabes que significa "[]" y "MOD". Al explicarlo con palabras sin usar esos "simbolos" la cosa se pone un poco oscura 😉
Saludos!
ahora si ya esta mucho mas claro!! muchisimas gracias!!!!!! exelente nota!!! 🙂
disculpa jeje! en el mismo ejemplo pusiste 68MOD7, en ves de 68MOD12. Si que esta complicada esta nota jajaja! saludos
"¿Te animas a calcular que día de la semana fue cuando naciste?"
No gracias. Paso de armarme un cacao mental. Sigo prefiriendo el método tecnológico.
cacao menal?…método tecnológico?..a ver ..si no es ningún método!!!…celebro que elijas la simplicidad, pero no es la simplicidad lo que nos tiene donde estamos, sino la curiosidad + la inteligencia……y sii… por supuesto que también la tienes…asi q… te animas a usarla?….
Te olvidas de la pereza. Sin la pereza tal vez no existiese el control remoto, los automoviles, etc.
Por cierto esto ye me lo sabia, en mi escuela vendian unos calendarios ”mágicos” que usaba un algoritmo parecido… Nací un 13, un viernes 13!! xDD.
Con el método tecnológico me refiero a consultar el calendario de un PC, móvil o agenda electrónica.
Sí, tengo inteligencia, y con un C.I. por encima de la media, pero paso de hacerme líos calculando semejante fórmula mentalmente, máxime cuando hay que tener en cuenta unos cuantos "peros" para que funcione correctamente.
cronosferatu: si combinas la vaguedad con la inteligencia te sale un genio.
Por mas que trato de calcular para el 27 de Marzo de 1980 no me da el dia exacto, aparte que me es confuso el "0" para marzo.
No entiendo nada, no es tan facil como dices ariel, toca tirarle cabeza de todas formas
No soy bueno para las matematicas ni siquiera me gustan las matematicas pero este articulo me pareció muy interesante 🙂
imposible que me lo aprenda estos algoritmos ahorita, mejor me lo guardo y mas luego lo repaso unas cuantas veces mas
Arieeel!!! una pregunta: en el post dices
" el valor de “y” es 68, que al dividir entre 12 nos da 5, con resto 8. IMPORTANTE: Ese resto de "8" es equivalente calcular "68 MOD 7" (68 módulo 7) "
Me parce que 68 MOD 7 =/= 8 y sería 68 MOD 12 = 8 o me equivoco???
" el valor de “y” es 68, que al dividir entre 12 nos da 5, con resto 8. IMPORTANTE: Ese resto de "8" es equivalente calcular "68 MOD 12" (68 módulo 12) "
gracias por el articulo…
Corregido! Gracias!
Yo conocia una forma para saberlo mucho mas sencillo y facil. Sin usar eso de MOD o [].
a practicar! :()
Un comentario de ayuda, si os habias dado cuenta esto sobraba, pero yo no me percatee de ello cuando lo hice:
Los dias de 2 enero y 13 febrero corresponder al año siguiente, asi que para calcular la fecha de febrero hay que calcularlo con el doomsday del año anterior o bien resulta mas facil memorizar el 0 de marzo que es el ultimo dia de febrero y el 3 de enero para años normales y 4 de enero para bisiestos.
Para saber si un año es bisiesto lo sabremos por el valor de ‘q’.
Si ‘q’ = 0, 4 o 8 tratamos con un año bisiesto.
Enero (años normales) 3, 10, 17, 24, y 31
Enero (años bisiestos) 4, 11, 18, y 25
Febrero (años normales) 7, 14, 21, y 28
Febrero (años bisiestos) 1, 8, 15, 22, y 29
…..
…..
Enero del año siguiente 2, 9, 16, 23, y 30
Febrero del año siguiente 6, 13, 20,y 27
Esto es para gente que no tiene nada que hacer……. como yo por ejemplo y buscamos divertirnos de una forma mas relajada y entretenida.
Buena y saludos.
Tirando un día al azar hay más de 14% de probabilidades de pegarle, creo que hacer el algoritmo con la mente daría una probabilidad del 90% de error, por lo tanto es 4% más confiable adivinarlo jajaj
Algoritmo para encontrar el día de la semana de una fecha determinad
1.Restar 1 al año si la fecha a buscar es antes de nuestra era, “aC ó dC”.
2.Restar 1 al año si el mes de la fecha a buscar está dentro del mes de enero o febrero.
3.Obtener el día de juicio con la siguiente formula
dj = (año + truncar( año / 4) ) mod 7
4.Para obtener los días transcurridos del 1 marzo, que es nuestro punto de referencia, hasta la fecha que buscamos es
dt = truncar (((mes + 9) mod 12 ) * (337 / 11)) – truncar((((mes + 9) mod 12 ) mod 5 ) / 4) + día
5.Obtenemos el residuo de los días transcurridos que son los días restantes dr = dt mod 7
6.Y por último sumas los días y sacas de nuevo el residuo y obtendrás el día de la semana
ds = (dj + dr) mod 7
El resultante será un número de entre 0 y 6 donde 0 es lunes, 1 martes, 2 miércoles, 3 jueves, 4 viernes, 5 sábado, y 6 domingo.
Invito a la gente que calcule el dia que fue el 31 de diciembre de 1999
me costó bastante pero ya me sale!
muchas gracias por la nota
Disculpad, pero pero para realizarlo, mentalmente, poseo una fórmula muy rápida y efectiva. 1º Tenemos que dividir las dos últimas cifras del año entre 4, tomar la parte entera de la división y despreciar el resto. 2º Aprenderse esta tabla para los meses del año:
0332-1462-5035, es decir un número para cada mes.
3º Aprenderse los números que corresponde a cada siglo:
1600-6, 1700-4, 1800-2, 1900-0, 2000-6, 2100-4, 2200-2- 2300-0, etc.
Resumen: Aplicar cada caso y sumar las cuatro partidas y el resultado dividir entre 7 para ver el día de la semana.
El primer ejemplo: 14-octubre-1968
68:4= 17. A octubre le correponde = 0.Al año 1968 le corresponde = 0
Sumamos: 17+0+68+0 = 85 85: 7 = 1 (Lunes).
El 14 de octubre de 1968 fue LUNES. ¡Fantástico, verdad!
Espero vuestras opiniones, pero con mi fórmula antes de un minuto resuelvo cualquier dia de la semama de cualquir siglo. UN SALUDO.
Disculpad, pero pero para realizarlo, mentalmente, poseo una fórmula muy rápida y efectiva. 1º Tenemos que dividir las dos últimas cifras del año entre 4, tomar la parte entera de la división y despreciar el resto. 2º Aprenderse esta tabla para los meses del año:
0332-1462-5035, es decir un número para cada mes.
3º Aprenderse los números que corresponde a cada siglo:
1600-6, 1700-4, 1800-2, 1900-0, 2000-6, 2100-4, 2200-2- 2300-0, etc.
Resumen: Aplicar cada caso y sumar las cuatro partidas y el resultado dividir entre 7 para ver el día de la semana.
El primer ejemplo: 14-octubre-1968
68:4= 17. A octubre le correponde = 0.Al año 1968 le corresponde = 0
Sumamos: 17+0+68+0 = 85 85: 7 = 1 (Lunes).
El 14 de octubre de 1968 fue LUNES. ¡Fantástico, verdad!
Espero vuestras opiniones, pero con mi fórmula antes de un minuto resuelvo cualquier dia de la semama de cualquir siglo. UN SALUDO.
Disculpad, pero pero para realizarlo, mentalmente, poseo una fórmula muy rápida y efectiva. 1º Tenemos que dividir las dos últimas cifras del año entre 4, tomar la parte entera de la división y despreciar el resto. 2º Aprenderse esta tabla para los meses del año:
0332-1462-5035, es decir un número para cada mes.
3º Aprenderse los números que corresponde a cada siglo:
1600-6, 1700-4, 1800-2, 1900-0, 2000-6, 2100-4, 2200-2- 2300-0, etc.
Resumen: Aplicar cada caso y sumar las cuatro partidas y el resultado dividir entre 7 para ver el día de la semana.
El primer ejemplo: 14-octubre-1968
68:4= 17. A octubre le correponde = 0.Al año 1968 le corresponde = 0
Sumamos: 17+0+68+0 = 85 85: 7 = 1 (Lunes).
El 14 de octubre de 1968 fue LUNES. ¡Fantástico, verdad!
Espero vuestras opiniones, pero con mi fórmula antes de un minuto resuelvo cualquier dia de la semama de cualquir siglo. UN SALUDO.
Disculpad, pero pero para realizarlo, mentalmente, poseo una fórmula muy rápida y efectiva. 1º Tenemos que dividir las dos últimas cifras del año entre 4, tomar la parte entera de la división y despreciar el resto. 2º Aprenderse esta tabla para los meses del año:
0332-1462-5035, es decir un número para cada mes.
3º Aprenderse los números que corresponde a cada siglo:
1600-6, 1700-4, 1800-2, 1900-0, 2000-6, 2100-4, 2200-2- 2300-0, etc.
Resumen: Aplicar cada caso y sumar las cuatro partidas y el resultado dividir entre 7 para ver el día de la semana.
El primer ejemplo: 14-octubre-1968
68:4= 17. A octubre le correponde = 0.Al año 1968 le corresponde = 0
Sumamos: 17+0+68+0 = 85 85: 7 = 1 (Lunes).
El 14 de octubre de 1968 fue LUNES. ¡Fantástico, verdad!
Espero vuestras opiniones, pero con mi fórmula antes de un minuto resuelvo cualquier dia de la semama de cualquir siglo. UN SALUDO.
Disculpad, pero pero para realizarlo, mentalmente, poseo una fórmula muy rápida y efectiva. 1º Tenemos que dividir las dos últimas cifras del año entre 4, tomar la parte entera de la división y despreciar el resto. 2º Aprenderse esta tabla para los meses del año:
0332-1462-5035, es decir un número para cada mes.
3º Aprenderse los números que corresponde a cada siglo:
1600-6, 1700-4, 1800-2, 1900-0, 2000-6, 2100-4, 2200-2- 2300-0, etc.
Resumen: Aplicar cada caso y sumar las cuatro partidas y el resultado dividir entre 7 para ver el día de la semana.
El primer ejemplo: 14-octubre-1968
68:4= 17. A octubre le correponde = 0.Al año 1968 le corresponde = 0
Sumamos: 17+0+68+0 = 85 85: 7 = 1 (Lunes).
El 14 de octubre de 1968 fue LUNES. ¡Fantástico, verdad!
Espero vuestras opiniones, pero con mi fórmula antes de un minuto resuelvo cualquier dia de la semama de cualquir siglo. UN SALUDO.
Disculpad, pero pero para realizarlo, mentalmente, poseo una fórmula muy rápida y efectiva. 1º Tenemos que dividir las dos últimas cifras del año entre 4, tomar la parte entera de la división y despreciar el resto. 2º Aprenderse esta tabla para los meses del año:
0332-1462-5035, es decir un número para cada mes.
3º Aprenderse los números que corresponde a cada siglo:
1600-6, 1700-4, 1800-2, 1900-0, 2000-6, 2100-4, 2200-2- 2300-0, etc.
Resumen: Aplicar cada caso y sumar las cuatro partidas y el resultado dividir entre 7 para ver el día de la semana.
El primer ejemplo: 14-octubre-1968
68:4= 17. A octubre le correponde = 0.Al año 1968 le corresponde = 0
Sumamos: 17+0+68+0 = 85 85: 7 = 1 (Lunes).
El 14 de octubre de 1968 fue LUNES. ¡Fantástico, verdad!
Espero vuestras opiniones, pero con mi fórmula antes de un minuto resuelvo cualquier dia de la semama de cualquir siglo. UN SALUDO.
Disculpad, pero pero para realizarlo, mentalmente, poseo una fórmula muy rápida y efectiva. 1º Tenemos que dividir las dos últimas cifras del año entre 4, tomar la parte entera de la división y despreciar el resto. 2º Aprenderse esta tabla para los meses del año:
0332-1462-5035, es decir un número para cada mes.
3º Aprenderse los números que corresponde a cada siglo:
1600-6, 1700-4, 1800-2, 1900-0, 2000-6, 2100-4, 2200-2- 2300-0, etc.
Resumen: Aplicar cada caso y sumar las cuatro partidas y el resultado dividir entre 7 para ver el día de la semana.
El primer ejemplo: 14-octubre-1968
68:4= 17. A octubre le correponde = 0.Al año 1968 le corresponde = 0
Sumamos: 17+0+68+0 = 85 85: 7 = 1 (Lunes).
El 14 de octubre de 1968 fue LUNES. ¡Fantástico, verdad!
Espero vuestras opiniones, pero con mi fórmula antes de un minuto resuelvo cualquier dia de la semama de cualquir siglo. UN SALUDO.
Disculpad, pero pero para realizarlo, mentalmente, poseo una fórmula muy rápida y efectiva. 1º Tenemos que dividir las dos últimas cifras del año entre 4, tomar la parte entera de la división y despreciar el resto. 2º Aprenderse esta tabla para los meses del año:
0332-1462-5035, es decir un número para cada mes.
3º Aprenderse los números que corresponde a cada siglo:
1600-6, 1700-4, 1800-2, 1900-0, 2000-6, 2100-4, 2200-2- 2300-0, etc.
Resumen: Aplicar cada caso y sumar las cuatro partidas y el resultado dividir entre 7 para ver el día de la semana.
El primer ejemplo: 14-octubre-1968
68:4= 17. A octubre le correponde = 0.Al año 1968 le corresponde = 0
Sumamos: 17+0+68+0 = 85 85: 7 = 1 (Lunes).
El 14 de octubre de 1968 fue LUNES. ¡Fantástico, verdad!
Espero vuestras opiniones, pero con mi fórmula antes de un minuto resuelvo cualquier dia de la semama de cualquir siglo. UN SALUDO.
Disculpad, pero pero para realizarlo, mentalmente, poseo una fórmula muy rápida y efectiva. 1º Tenemos que dividir las dos últimas cifras del año entre 4, tomar la parte entera de la división y despreciar el resto. 2º Aprenderse esta tabla para los meses del año:
0332-1462-5035, es decir un número para cada mes.
3º Aprenderse los números que corresponde a cada siglo:
1600-6, 1700-4, 1800-2, 1900-0, 2000-6, 2100-4, 2200-2- 2300-0, etc.
Resumen: Aplicar cada caso y sumar las cuatro partidas y el resultado dividir entre 7 para ver el día de la semana.
El primer ejemplo: 14-octubre-1968
68:4= 17. A octubre le correponde = 0.Al año 1968 le corresponde = 0
Sumamos: 17+0+68+0 = 85 85: 7 = 1 (Lunes).
El 14 de octubre de 1968 fue LUNES. ¡Fantástico, verdad!
Espero vuestras opiniones, pero con mi fórmula antes de un minuto resuelvo cualquier dia de la semama de cualquir siglo. UN SALUDO.
Disculpad, pero pero para realizarlo, mentalmente, poseo una fórmula muy rápida y efectiva. 1º Tenemos que dividir las dos últimas cifras del año entre 4, tomar la parte entera de la división y despreciar el resto. 2º Aprenderse esta tabla para los meses del año:
0332-1462-5035, es decir un número para cada mes.
3º Aprenderse los números que corresponde a cada siglo:
1600-6, 1700-4, 1800-2, 1900-0, 2000-6, 2100-4, 2200-2- 2300-0, etc.
Resumen: Aplicar cada caso y sumar las cuatro partidas y el resultado dividir entre 7 para ver el día de la semana.
El primer ejemplo: 14-octubre-1968
68:4= 17. A octubre le correponde = 0.Al año 1968 le corresponde = 0
Sumamos: 17+0+68+0 = 85 85: 7 = 1 (Lunes).
El 14 de octubre de 1968 fue LUNES. ¡Fantástico, verdad!
Espero vuestras opiniones, pero con mi fórmula antes de un minuto resuelvo cualquier dia de la semama de cualquir siglo. UN SALUDO.
jajajaajajaajaja q vien
q el fin del mundo lle garA MUY PRON TO Y LUEGO Q LLEGE EL FIN DEL MUNDO TODOS CORRERAN DEL SUSTO LOS Q AN PECADO SE ARREPENTIRAN PERO NO LOS VAN A PERDONAR POR Q LLA FUE MUY TARDE Y LOS Q TUVIERON LA FE DE DIOS SEGIRAN RRESANDO COMO SIENPRE LO AN ECHO Y ELLOS NO VAN A ESTAR ASUSTADOS POR Q AMAS DE Q ESTEN ASUSTADOS DAN GRACIAS Q LLEGO EL MOMENDO DE IR A DON DE PERTENESEN Y DONDE VAN A ESTAR JUNTO A DIOS PERO LOS Q ODIAN A DIOS VAN A TENER DE CASTIGO EL IN FIERNO DON DE SATANAS Y SUS DIADLOS POR ESO MEJOR DEJEN Q DIOS EN TRE ES SU CORAZON TEMPRANO ATENTA MENTE JOSE GARCES……………….?¿
Tengo una duda respecto a sus comentarios estoy haciendo un programa que calcule el dia de dicha y además los dias siguientes y anteriors a este. Mi duda es con respecto a lo que alguien comento de los años bisiestos si la fecha que quiero calcular cae en un año bisiesto ya no aplica porque tendría que restarle un dia al doomsday! para que me resulte 🙁 No entendi muy bien esa parte podrían explicarme pofavor muchas gracias.
Tengo una duda respecto a sus comentarios estoy haciendo un programa que calcule el dia de dicha y además los dias siguientes y anteriors a este. Mi duda es con respecto a lo que alguien comento de los años bisiestos si la fecha que quiero calcular cae en un año bisiesto ya no aplica porque tendría que restarle un dia al doomsday! para que me resulte 🙁 No entendi muy bien esa parte podrían explicarme pofavor muchas gracias.
¿Qué sentido tiene usar los días de la semana? Mira que nos complicamos los humanos.
tengo un colega con Asperger a quien siempre le preguntamos las fechas y nos dice que día de la semana fue, adicionalmente de cuenta algunas noticias resaltantes de esa fecha, al preguntarle cual era su “truco” tranquilamente respondía que no había tal truco, sino que recordaba todo los periódicos que había leído desde X fecha de 1972, que solo tenia que buscar en su mente la portada y allí le aparecía todo.
pd: tardó mas de 15 años en titularse ne la universidad debido a que a pesar de tener una memoria fotográfica excepcional, tiene muchas carencias a la hora de elaborar material propio o responder cosas que necesiten razonamiento.