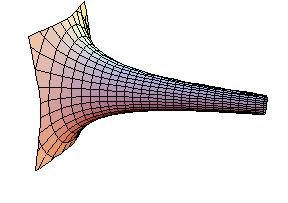
Existen curiosos objetos que poseen propiedades lo suficientemente extrañas como para resultar atractivas para los matemáticos. Uno de los más conocidos es el cuerno de Gabriel, a veces llamado Trompeta de Torricelli, una figura geométrica que a pesar de tener una superficie infinita posee un volumen finito. Ideada por Evangelista Torricelli, este objeto ha dado lugar a una paradoja interesante: se necesitaría una cantidad infinita de pintura para pintar su interior pero, a la vez, sería posible llenar ese espacio finito con algunos litros de pigmento, cubriendo así su superficie.
¿Puede una superficie infinitamente grande encerrar un área finita? A primera vista, suena como algo imposible. Pero así como los fractales demostraron que era posible tener una “linea costera” infinitamente larga rodeando un área finita, también es posible encerrar un volumen finito utilizando una “cáscara” infinitamente grande. A pesar de ello, no hay una gran cantidad de objetos que cumplan con estas premisas, y uno de los más conocidos es el cuerno de Gabriel, ideado por Evangelista Torricelli hace más de 350 años.
Esta figura geométrica, a la que algunos también suelen llamar Trompeta de Torricelli, fue en principio considerada una paradoja. Es que para pintar una superficie infinita hace falta, por más delgada que intentemos hacer la capa de pigmento, una cantidad infinita de pintura. Si un pintor que contase con un tiempo infinito para encarar la tarea intententase pintar un cuerno de Gabriel, descubriría que no hay en el universo espacio suficiente para almacenar la cantidad de pintura que tendría que usar. Pero por otra parte, dado que su volumen es finito, cualquier mortal podría llenarlo con una cantidad finita de pintura. ¿Dónde está la paradoja? En que al llenar la Trompeta de Torricelli con pintura obviamente estamos pintando su interior, el mismo que hace un momento descubrimos era imposible de pintar.
Sin embargo, hay algunos fallos en este razonamiento. En primer lugar, es imposible construir un artefacto semejante, ya que no hay material suficiente para ello, y si lo hubiese, el tiempo que insumiría esta tarea sería infinito. Pero aun si existiese, la capa de pintura utilizada debería tener un grosor constante y finito. Esto es imposible de lograr en el interior del cuerno, ya que la mayor parte de la longitud de la figura (el extremo que queda a la derecha en la imagen anterior) no es accesible a la pintura, porque rápidamente su diámetro se hace menor al del una molécula de pintura. Y si alguien lograse inventar una “pintura mágica” formada por átomos y moléculas sin grosor (derribando la estructura de toda la física que conocemos), necesitaríamos una cantidad infinita de tiempo para que ésta llegase hasta el final del cuerno.
Supongamos que podemos dejar de lado los problemas prácticos que trae aparejado la construcción de este artefacto, y concentrémonos en sus propiedades teóricas. El diámetro interior del cuerno tiende a cero, y los matemáticos actuales saben que cuando esto ocurre, el espesor de la capa de pintura forzosamente debería ser igual o menor a un valor determinado. No vamos a describir el cálculo aquí, pero puede demostrarse que la cantidad de “pintura mágica” necesaria se obtiene mediante una integral impropia, cuyo resultado es finito, y que a partir de un determinado punto, una simple gota de pintura alcanzaría para cubrir el resto de la superficie de la trompeta, por más que su longitud y superficie sea infinita.
En pocas palabras, y aunque sin tener las herramientas matemáticas adecuadas pueda parecer lo contrario (¡maldito sentido común!) el hecho de que la superficie de la trompeta sea infinita no implica que la cantidad de pintura para cubrirla deba ser infinita también, destruyendo la aparente paradoja. ¿Cual es la utilidad práctica de todo esto? Probablemente ninguna. Pero a veces resulta divertido encontrarse con estos viejos problemas que estimulan nuestra imaginación. ¿No crees?