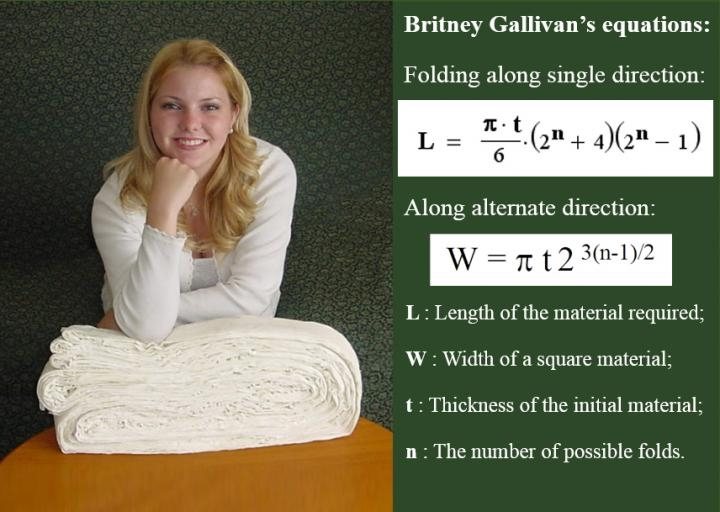Una hoja doblada 400 veces y el crecimiento exponencial

Uno de los aspectos matemáticos que más asombra y confunde a la gente es el crecimiento exponencial. Existen diferentes formas de comprobar sus efectos, pero una de las más sencillas requiere una hoja de papel. Ningún papel especial, con una hoja A4 será suficiente. La doblas una vez, y otra, y otra… hasta que no puedes más. La mayoría no logra pasar de los siete pliegues, y el récord es de doce usando papel higiénico. Entonces, ¿qué sucedería si de algún modo fuera posible doblar un papel 400 veces? La respuesta… ni siquiera tiene sentido.

Crecimiento exponencial y una hoja de papel

Ajedrez y granos de arroz. Si estás buscando un ejemplo clásico que te ayude a visualizar el crecimiento exponencial, ese es ideal. Lo que parecía una recompensa ridícula para el rey terminó convirtiéndose en una pesadilla de agricultura. Miles de años después, desconocemos el destino del inventor. De hecho, algunos dudan sobre la legitimidad de la historia, pero es impecable como curiosidad matemática. Ahora, ¿qué tal suena hacerlo en casa?

No me refiero a masacrar paquetes de arroz, sino a ver el crecimiento exponencial en primera persona. Todo lo que necesitas es una hoja de papel. Si es delgado te será más fácil trabajar al principio… pero sólo al principio.

El famoso límite de los siete pliegues es un mito. La estadounidense Britney Gallivan batió el récord con doce pliegues, y para ello necesitó una hoja única de papel higiénico de 1.200 metros de largo.

Un detalle a tener en cuenta es que sus pliegues fueron en la misma dirección, e implementó reglas estrictas para considerar al papel «doblado». Yo hoy propongo algo diferente: Suspender los límites de la física por un rato, y doblar un papel imaginario 400 veces.

• 0.1 milímetros de espesor, completamente indestructible.
• A los once pliegues, el espesor del papel ya es como una pelota de básquet.
• 14 pliegues, un ser humano promedio.
• 22 pliegues, más alto que el Empire State.
• 30 pliegues, y el papel ya está en el espacio.
• 37 pliegues superan el diámetro de la Tierra.
• 42 pliegues llegan a la Luna.
• 50 nos llevan al Sol.
• 66 pliegues equivalen a un año luz.
• 68 a la distancia entre el Sol y Próxima Centauri.
• 83 pliegues cubren la Vía Láctea de un extremo al otro.
• 97 pliegues y estamos en la galaxia de Andrómeda.
• Todo el supercúmulo de Virgo entra en 93 pliegues.
• El Universo Observable se nos termina en «apenas» 103 pliegues.
• A los 133 pliegues, el papel supera mil millones de veces el largo de todo el universo.
• Al ser doblado 346 veces, el papel tiene un espesor idéntico al de un gúgol, 10^100 metros.
• Y al alcanzar los 400 pliegues, superamos a ese mismo número… pero en años luz.

En resumen, el resultado es inconcebible incluso para nuestra realidad.